문제
한수는 크기가 2^N × 2^N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다.

N > 1인 경우, 배열을 크기가 2^N-1 × 2^N-1로 4등분 한 후에 재귀적으로 순서대로 방문한다.
다음 예는 2^2 × 2^2 크기의 배열을 방문한 순서이다.

N이 주어졌을 때, r행 c열을 몇 번째로 방문하는지 출력하는 프로그램을 작성하시오.
다음은 N=3일 때의 예이다.

입력
첫째 줄에 정수 N, r, c가 주어진다. (1 ≤ N ≤ 15, 0 ≤ r, c < 2^N)
출력
r행 c열을 몇 번째로 방문했는지 출력한다.
문제 풀이
Z 모양으로 탐색했을 때 r행 c열을 몇 번째로 방문하는지 맞추는 문제이다.
처음에는 2차원 배열을 만들어 문제를 해결하려고 했으나
문제에서 주어진 조건의 최대값인 2의 15제곱만큼 배열을 만들면 문제가 너무 복잡해진다.
따라서 분할정복, 재귀 두 가지 방법을 이용해 문제를 해결해보았다.
1. 분할정복
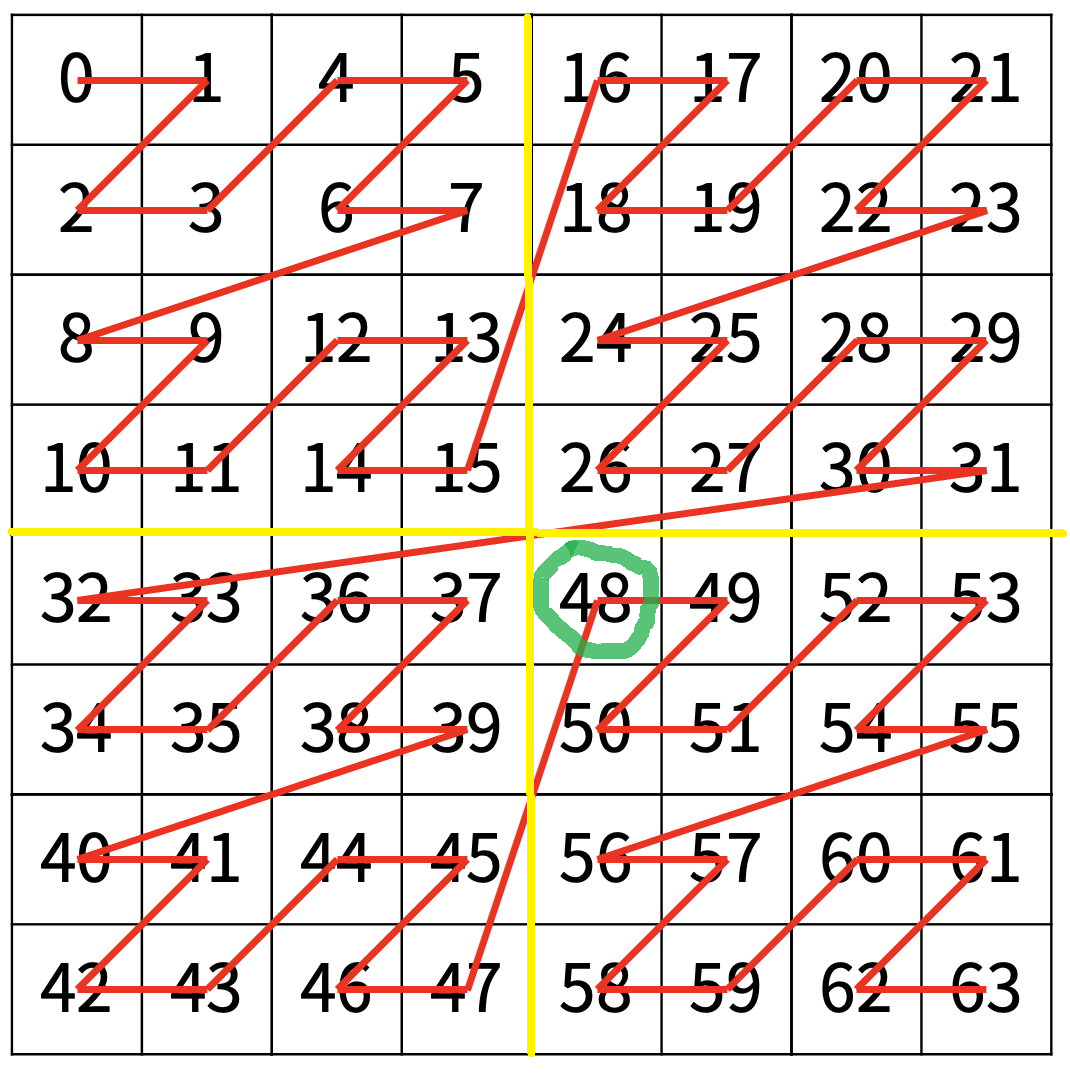
N=3 일 때의 경우에서 (7, 7)을 몇 번째로 방문했는지 알아내는 과정을 예로 들면,
먼저 위의 그림과 같이 4등분으로 분할해준다.
그런 다음 (7, 7)이 몇 사분면에 속해있는지 확인한 후 속해있는 사분면의 첫번째 값을 더해준다.
이때, 각 사분면의 첫번째 수는 0, 16, 32, 48인데 이 수는 분할한 후 배열 크기의 배수이다.
즉, 분할 후 N=2이므로 배열의 크기는 2^2 x 2^2 = 16이다.
1사분면을 제외하고 각 사분면의 첫 숫자는 16의 배수이다.

그 후, 위 그림과 같이 분할을 반복하며 (7, 7)이 속하는 사분면의 첫 번째 수를 더해주면 답을 구할 수 있다.
분할을 반복할 때 0번째로 방문하는 위치가 분할 한 후의 배열로 바뀌므로
r과 c의 값을 그에 맞게 변경해주어야 한다.
분할 후 (7, 7)은 2^2 x 2^2 배열에서 (3, 3)이 된다. 즉, 2^2 = 4를 각각 뺀 값이다.
분할 후 (3, 3)은 2^1 x 2^1 배열에서 (1, 1)이 된다.
또한 0번째의 위치도 분할 후의 배열의 가장 왼쪽 맨 위로 바뀌므로
그에 맞는 첫 번째 수를 동일하게 구해 더해주면
48 + 12 + 3 = 63이 된다.
2. 재귀
(1, 0) -> (2, 0)는 2 -> 8
(2, 0) -> (4, 0)는 8 -> 32
(1, 2) -> (2, 4)는 6 -> 24
(2, 1) -> (4, 2)는 9 -> 36
위와 같이 좌표가 2배가 되면 방문 순서가 4배가 되는 것을 알 수 있다.
따라서 이를 이용해 재귀 함수를 만들 수 있다.
어떤 좌표를 각각 2로 나눈 몫에 해당하는 값에 4를 곱하면 현재 위치의 값을 구할 수 있다.
이때, 주의해야할 점은 만약 현재 위치가 4의 배수가 아닐 수 있으므로 현재 위치가 4의 배수로부터
얼마나 지난 위치에 있는지를 구해줘야 한다.
문제에서 주어진 예시를 보면 2 x 2로 모두 분할했을 때, 각각 첫번째 수가 4의 배수라는 것을 알 수 있다.
| 0 | 1 |
| 2 | 3 |
| (0, 0) | (0, 1) |
| (1, 0) | (1, 1) |
60으로 예를 들었을 때, 60 나누기 4는 15이고 15는 4의 배수가 아니며 위의 표에서 3번째 위치에 위치한다. 따라서 3을 더해주면 된다.
이처럼 4의 배수로부터 현재의 위치를 구하는 식은 2 * (r % 2) + (c % 2)로 구할 수 있다.
My Code 1 - 분할 정복
N, r, c = map(int, input().split())
res = 0
while N != 0:
N -= 1 # 4등분으로 분할
# 1사분면에 속할 때
if r < (2 ** N) and c < (2 ** N):
res += 0
# 2사분면에 속할 때
elif r < (2 ** N) and c >= (2 ** N):
res += (2 ** N) * (2 ** N) * 1
c -= (2 ** N)
# 3사분면에 속할 때
elif r >= (2 ** N) and c < (2 ** N):
res += (2 ** N) * (2 ** N) * 2
r -= (2 ** N)
# 4사분면에 속할 때
else:
res += (2 ** N) * (2 ** N) * 3
r -= (2 ** N)
c -= (2 ** N)
print(res)My Code 2 - 재귀
N, r, c = map(int, input().split())
def func(N, r, c):
if N == 0:
return 0
else:
return 2 * (r % 2) + (c % 2) + 4 * (func(N - 1, r // 2, c // 2))
print(func(N, r, c))'백준(Python) 풀이' 카테고리의 다른 글
| 백준 11723번. 집합 (Python / 파이썬) (0) | 2022.07.07 |
|---|---|
| 백준 1620번. 나는야 포켓몬 마스터 이다솜 (Python / 파이썬) (0) | 2022.07.07 |
| 백준 10250번. ACM 호텔 (Python / 파이썬) (0) | 2022.07.05 |
| 백준 1874번. 스택 수열 (Python / 파이썬) (0) | 2022.05.03 |
| 백준 1654번. 랜선 자르기 (Python / 파이썬) (0) | 2022.05.03 |

댓글